
James Miller G3RUH
Without an atmosphere, Oscar-13 would collide with the Earth's crust on 1997 Feb 03. This is due to the pull of the Sun and Moon; the orbit eccentricity is increasing and that reduces perigee height.
But the presence of Earth's atmosphere at perigee robs AO-13 of energy, which is dissipated in the form of heat. This will cause burn-up around mid-December 1996.
End-of-life effects are discernible as a) orbital period decrease and b) changes of attitude, c) heating. The first two are already observable.
Aspects of AO-13's re-entry are explored in these notes. In particular a re-orientation to the unfamiliar attitude Alon/Alat = 90/0 is proposed from mid-August 1996.
This article is in two sections. The second provides a detailed numerical basis for understanding this re-entry scenario.
Orbital Period
This article was written in late May 1996, seven months prior to AO-13's demise. The orbital eccentricity, presently 0.74 continues to increase slowly towards its zenith value of 0.745 in the first week of September 1996. Thereafter drag augments the luni-solar forces, circularising the orbit, with burn-up some three months later.
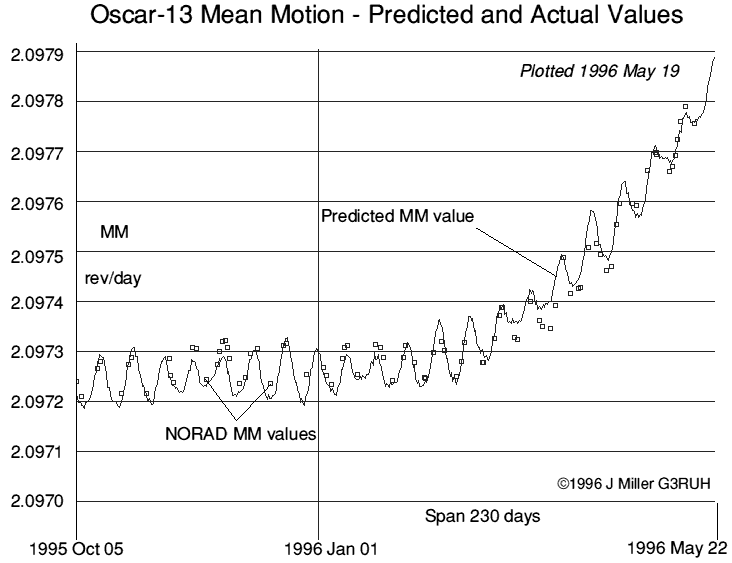
But even now, if you study the AO-13 keplerian elements and compare mean motion for 1996 January with the mean motion for 1996 April, it's increased from a value of 2.09725 rev/day to 2.09750 rev/day in just three months. This is equivalent to a reduction in period of 80 ms/orbit, and it's already noticeable how badly actual AOS and LOS times compare with predictions if you're using stale keplerian elements. This change in period is caused by atmospheric drag at each perigee encounter.

Figure 1. The predicted values of Mean Motion and other elements are based a model that includes a best estimate of the aerodynamic profile of the satellite. Forces modelled are Earth's gravity up to degree 8, zonal, tesseral and sectoral terms from the GEM10B model, Sun, Moon, drag using US Standard Atmosphere 1976 and solar radiation pressure.
Fine details of orbital period and other keplerian elements for AO-13 have already been published [2,3].
Heating Effects
Heating is not yet observable as of 1996 May. At 300 km altitude it's tiny, just +0.2C extra on the solar panels. The temperature sensor resolution is 0.6C, and radiation from the Earth at perigee warms the panels by about 9C. Both these factors presently swamp any nuances due to friction.
Around 1996 September the solar panels could heat up by an additional +5C at perigee, which will be easy to detect.
Later, in November, heating will become extreme, resulting in spacecraft failure due to damage and/or melting of antennas and solar panels.
Attitude Changes
A more subtle effect is apparent in the spacecraft's attitude. AO-13 is spin stabilised, and should unswervingly point towards the same point in space.
We can measure AO-13's orientation by several different methods. One is based on measuring the off-pointing angle of the S-band antenna using its beacon frequency modulation [4]. By doing this a few times each orbit and for a few orbits, the satellite's orientation can be determined to about 5 degrees precision.
Now, given the satellite's orientation, one can predict the future Sun angle (the angle between Sun and solar panels). We find that predictions and measurements do not agree. They diverge by 0.1°/perigee. (Perigee altitude = 320 km, 1996 May).
The reason for this discrepancy is that the spacecraft's orientation is actually changing. The satellite passes through the upper atmosphere every perigee. AO-13 is not symetric as seen sideways on. The motor sticks out, and picks up an eccentric force Fx which applies a torque (twist) to the satellite, and slews the spin axis up out of the orbit plane 0.1° every pass.
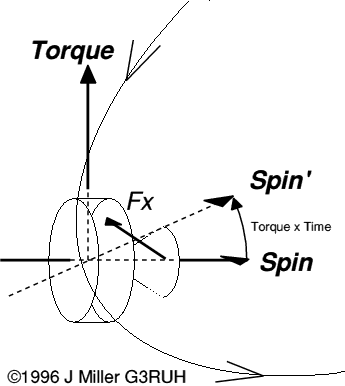
Figure 2. Windage on the motor extension causes AO-13's orientation to change. See text.
Clearly this can only get worse. At some point the attitude will change several degrees each perigee, and eventually precess whole revolutions at a time, effectively leaving a random re-orientation in attitude latitude after each encounter. The will render transponding useless and command very difficult. The best solution is a final re-orientation to ALON/ALAT 90/0, plus a spin- up for additional stability some time from mid August '96 onwards. Sun angle constraints require this be done anyway by 1996 Nov 02.
Environment in Detail
I cannot pretend yet to be an expert in the ballistics of irregular structures travelling at Mach 13 through a near vacuum. My understanding of the kinetic theory of gases, available in any physics text, provides the basis for what follows.
The numbers that characterise the drag problem are so enormous or so microscopic that they're hard to imagine. But with a little normalisation we can render them in familiar terms.
Atmospheric Density
At sea level air weighs 1.2 kg/m3, which is comprehensible enough. The average spacing between molecules is 3.3 nm.
At an altitude of 100 km the mean spacing is 450 nm, about the same as the wavelength of red light or the width of a pit on a Compact Disc.
At 300 km, the atmospheric density is a mere 24 milligrams per cubic kilometre. Even at that low value, the molecules are packed at an average spacing of 13 µm, and you'd count 500x1012 molecules in a cubic metre. The mean free path, or average distance travelled before colliding with another molecule is however 6.6 km!
Mean Air Molecular Mean Free Kinetic
Altitude Density Spacing Path Temperature
km kg/m3 µm K
---------------------------------------------------------------
0 1.225 x100 0.003 0.13 nm 288
50 5.821 x10-4 0.04 0.3 mm 272
100 5.297 x10-7 0.5 0.3 m 204
150 2.070 x10-9 3 78 m 635
200 2.789 x10-10 6 580 m 859
300 2.418 x10-11 13 6.6 km 973
400 3.725 x10-12 24 43 km 993
500 6.967 x10-13 41 230 km 997
1000 3.019 x10-15 250 53000 km 1000
---------------------------------------------------------------
Table 1. Typical properties of Earth's atmosphere. Density above 100 km varies a lot, typically 2:1 to 3:1 either way at 300 km, more at higher altitudes. The collision cross section of a molecule is taken as 3 x 10-19 m2. Data from Wertz [1] appendix L3.
Forces
What makes these small densities significant of course, is the colossal speed of the spacecraft. This is typically 8000 m/s, so it collides with a lot of molecules per second, and the resulting drag forces are not insignificant.
In one second, an object of area A moving at speed V ploughs through a volume of A V cubic metres, and if that's full of material at density rho, the object collides with rho A V kilograms of matter per second, at a speed of V. The exchange of momentum decelerates the satellite with a force of order (rho A V) * V. Specifically, F = 1/2 Cd rho A V2 (Newton) where Cd is a dimensionless number typically 1 ~ 2 called the drag factor. It depends on the aerodynamic profile of the object.
Now though density is small that value V2 is a large number, and at 100 km altitude, an object of area 1 m2 experiences a force of order 17 N, equivalent to a weight of 1.7 kg on Earth. Given that AO-13 has a mass of 84 kg, this is a big force, relatively speaking, especially as the perigee encounter lasts a minute or two.
To put these forces into perspective, imagine AO-13 is put into a wind tunnel on Earth. We ask, what air speed is needed to exert the same force as AO-13 experiences in space when travelling at 8000 m/s? See Table 2.
Perigee Drag Air Speed for
Altitude Force/g Equal force
km kg m/s
----------------------------------
50 1900 170
60 1050 126
70 286 66
80 62 31
90 11 13
100 1.7 5.1
150 0.007 0.32
200 0.001 0.12
----------------------------------
Table 2. Shows the ground air speed which exerts the same force on a square metre as AO-13 experiences in space at 8000 m/s at various altitudes. g = 9.81 m/s2. For comparison, the speed of sound at sea level is 340 m/s. Blowing gently onto your hand is 0.3 m/s.
Heating
The work done per second by the drag force is given by P = F V , which from the previous section gives P = 1/2 Cd rho A V3 watts. This power is of course expended as heat.
A satellite's chief source of heat is the Sun, which arrives at a power flux of 1358 W/m2. So, to gain some insight as to the scale of additional warming we can compare the frictional heating of a 1 m2 object to the Solar radiation constant.
From another perspective, we can also ask what speed do we have to drag AO- 13 through the air at sea level to expend the same amount of power. See Table 3.
Perigee Normalised Speed for Altitude frictional Equal Power km heating m/s --------------------------------- 70 16532 326 80 3591 196 90 640 110 100 100 59 110 18 33 120 4.6 21 130 1.6 14 140 0.73 11 150 0.39 9.4 200 0.053 4.8 300 0.005 2.1 ---------------------------------Table 3. Shows the heat generated by drag on a 1 m2 object moving at 8000 m/s at various altitudes. This is normalised to 1358 W/m2, the Solar radiation constant. Also shown is the speed at which one expends the same amount of power overcoming drag at sea level. For example, at 100 km altitude a satellite receives 100x more heat than from the Sun alone, equivalent to the power expended towing it through the sea-level atmosphere at 59 m/s (132 mph).
Temperature
AO-13's normal thermal environment is very benign. It operates at shirt- sleeve temperatures throughout. The solar panels maintain 12C except during eclipses, internal temperatures are typically 15-25C.
But what can we expect to happen when additional frictional heating as per table 3 is apparent?
Of course, things will warm up to a temperature such that they re-radiate the extra heat. This is governed by the Stefan-Boltzmann law which states that the radiated power from a hot body is proportional to the fourth power of the absolute temperature. The constant of proportionality is 5.67 x 10- 8 W/m2/K4
Two items most vulnerable to excess heating are the solar panels and the antenna rods. If either fails, we lose our satellite.
Solar Panels
An AO-13 solar panel has an area of 0.183 m2, and delivers typically 8 watts of electrical power. Since the satellite is spinning, half the time a panel is in darkness, and even when illuminated, sunlight falls at an angle ranging from skimming to perpendicular. In fact the average illumination is 0.31 x Cos (Sun Angle) of the maximum possible. So taking a typical Sun angle of 20°, a panel receives 1358 x 0.31 x Cos(20) = 394 W/m2 of power. A panel is designed to reflect very little incident energy, say 5% (a guess) or 20 W/m2. The panel radiates to space from its outside surface, but receives some radiation from the spacecraft interior. Table 4 shows the full balance sheet:
Contribution W/m2
------------------------------------------ ------
Incident sunlight: 1358 x 0.31 x Cos(20): 394
Reflected sunlight: 5% x 394 -20
Converted to electricity: 8/0.183 -44
Radiation from interior Ti=20C to panel: 44
Radiation to space, Tp = 12C: -374
----
0
----
Table 4. Solar panel radiation balance, panel at 12C.
I promise that table 4 was not "fixed". I wrote down the power balance equation and solved it for an unknown panel temperature. It came out as 12C, the same as shows in the spacecraft telemetry. Changing the Sun angle to 0° produces 14.5C, also as telemetered.
Antenna Rods
The 2m hi-gain antenna elements stick out directly from the AO-13 body. So they cannot really "see" the warm spacecraft, only sunlight and space. They are made of thin concave tape, painted matt black. Since they are spinning, they receive only 64% (2/pi) of the maximum available sunlight, and they re-radiate heat from both sides. From this we deduce these elements' temperature is given by the balance of 0.64 x 1358 = 2 x 5.67 x 10-8 x T4 W/m2 and so T = 296K or 23C.
The 70 cm hi-gain antenna elements are are black cylindrical rods mounted on the top face of the satellite, and can see 30% warm structure and 70% space. They too receive 64% of the available sunlight, but re-radiate from pi x more area than is exposed to the Sun. Proceeding in a similar way to the forgoing shows the 70 cm antenna rods to be at 17C.
Frictional Heat
We can now repeat the forgoing exercises with extra heat due to drag. The results are shown in Table 5:
Perigee Solar 2m Hi 70cm Hi Approx Altitude Panel Gain Gain Date km C C C 1996 ------------------------------------------------ 300 12 23 17 May 25 200 14 26 19 Aug 09 180 16 30 22 Aug 30 160 21 38 28 Oct 11 150 27 48 35 Oct 27 140 37 65 48 Nov 01 130 62 102 76 Nov 13 120 119 181 141 Nov 18 110 249 345 283 Nov 26 100 511 663 564 Dec 07 90 969 1214 1055 Dec 11 80 1638 2014 1770 -- 70 2526 3078 2720 -- 60 3597 4360 3865 -- 50 4219 5105 4531 -- -----------------------------------------------Table 5. Equilibrium temperatures of components on AO-13 due to perigee frictional drag. Solder melts at 200-240C. Aluminium melts at 660C, and boils at 2500C. Spacecraft moving through atmosphere "sideways" on.
So for example, when perigee altitude is 180 km (1996 Aug 30), the solar panels will warm up from 12C to 16C, a rise of +4C which should be detectable in the telemetry. Whether or not the equilibrium temperatures are actually attained depends on the duration of heating power input.
Heating Profile
Perigee heating is short lived. It builds up to a peak, and then falls away in a matter of minutes. So we need to determine this profile to see whether components will reach the equilibrium temperatures predicted in table 5.
To do this one can seed a regular tracking program with the relevant keplerian elements and examine the satellite's speed at (say) 10 second intervals through a perigee encounter. This can be repeated for a selection of perigee heights.
Recalling table 3, we can say that perigee heating begins to be significant, in the sense of potentially damaging, when it exceeds 1 solar constant. That happens when perigee altitude is 135 km (1996 Nov 12) and below, and we can confine our interest to that regime. A typical heating profile is shown in figure 3.
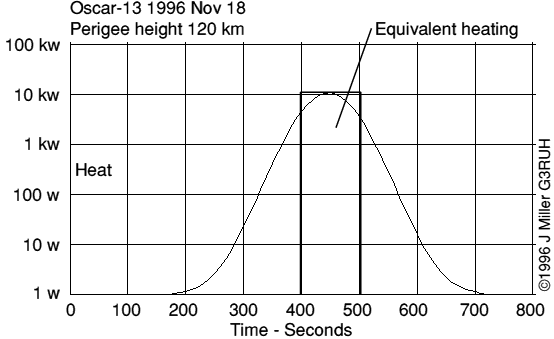
Figure 3. Heating profile for Oscar-13. Vertical axis is logarithmic. Equivalent heating time (Area/Peak) is 100 sec, for perigee altitude less than 130 km. See text.
The total energy expended is given by the area under the power curve, and dividing this by the peak value of the curve gives an equivalent heating time as though the peak were considered rectangular in profile.
This time turns out to be between 90 and 110 seconds, and is essentially independent of perigee altitude. This is a very useful index.
100 seconds is long enough for "flimsy" parts of the spacecraft, such as the 2m hi-gain tape antenna, to reach the equilibrium temperatures detailed in table 5.
Antennas
I wrote a simulation for the differential equations of temperature for the 2m hi-gain tape antenna. It shows that when exposed to 10 solar constants additional heat flux (1996 Nov 24), the antenna elements reach a steady state of 260C within 25 seconds. If heated by 100 solar constants (perigee altitude ~100 km, 1996 Dec 07) it reaches melting point after only 5 seconds exposure!
The 70cm hi-gain rods are relatively more massive. Simulation shows that exposed to an additional 10 solar constants of heat they reach 170C after 100 seconds. However, exposed to 100 solar constants they melt after 1 minute.
Solar Panels
I do not know the failure mode of solar panels when suddenly exposed to additional heat. Presumably thermal shock will cause cells to crack.
There are six independent panels, connected via diodes to the battery charge regulator. Each panel comprises three arrays, and each array is configured as 3 x 23 cells. A cell is 14.05mm high x 21.65mm wide. The panel voltage is typically 30 - 35 volts.
There is redundancy in this construction, so that single cell failure is not catastrophic. But one suspects that once cells begin to break, a critical number of others will also break within a very short time.
Let us suppose that a temperature rise to 300C breaks the panels. From table 5 this should occur at a perigee altitude of ~105 km, 1996 Nov 29, assuming a sideways presentation to the atmosphere. A "bottom" presentation would obviate this problem.
Attitude Changes
Earlier it was remarked that the attitude direction is no longer stable. This is attributed to aerodynamic forces acting on the motor extension. We see a 0.1°/perigee increase in ALAT, and this increase is cumulative. (Perigee altitude = 320 km, 1996 May). ALAT is the angle that the motor- antenna (spin) axis points up out of the orbit plane. Its nominal value is zero so that the satellite is Earth-centre pointing during the operational part of the orbit.
Whilst, 0.1°/perigee is minor, 1°/perigee would be an embarrassment. We can expect this to happen when perigee altitude is around 200 km, 1996 Aug 09, 3 months before any burn-up effects.
If we re-orient the satellite to ALON/ALAT=90/0 then the spacecraft presents bottom/motor to the atmosphere. This has the following benefits:
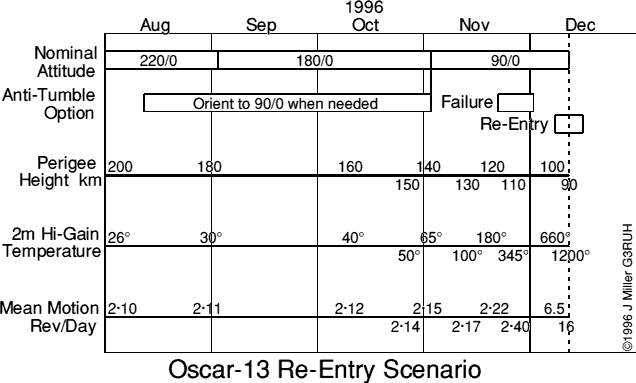
Figure 4. This bar chart summarises the final months of Oscar-13.
References
1. Wertz, J.R. (Ed), Spacecraft Attitude Determination and Control, D. Reidel Publishing Company, 1984, ISBN 90-277-1204-2.
2. J.R.Miller, The Re-Entry of Oscar-13, Proceedings of the 12th annual Amsat Space Symposium, Orlando, Florida, USA, 1994. Also: Oscar News (UK) 1994 Oct No. 109 p 16-20. Also: Jamsat Newsletter (JA) No. 166, 1995 March 25. p1-4. Also: Amsat-DL Journal (D), Jg. 22, No. 1, Mar/May 1995. Also: Amsat OZ Journal (OZ) No. 37, 1995 May. Also: The Amsat Journal (USA) Vol 18 No.3, May/June 1995. WWW includes a listing of the numerical integration.
3. J.R.Miller, AO-13 Re-Entry Keplerian Elements, Oscar News (UK) 1995 Oct No. 115 p36-37. Also: Satellite Operator (US), 1995 July, p11-12. Elements. General archive.
4. J.R.Miller, Measure AO-13 Squint Directly!, The Amsat Journal (USA) Vol 16 No. 1, January 1993. Also: Oscar News (UK) 1993 Feb No. 99 p26-28. Also: Amsat-DL Journal (D), Jg. 20, No. 1, March 1993. Also: Amsat-VK Newsletter (VK), No. 94, February 1993.
Feedback on these pages to Webmaster. Feedback on the article should be sent to James Miller
Created: 1995 Feb 11 -- Last modified: 2023 Apr 13