
James Miller G3RUH
Geostationary satellites have on-board thrusters to compensate for these inescapable deviations. But Oscar-13 does not, and its orbital eccentricity is now (1994) monotonically increasing, with an attendant decrease in the height of perigee. When this height reaches a little under 200 km, atmospheric drag becomes significant, converting the satellite's energy into heat and slowing it down.
Thus each subsequent apogee is slightly lower and gradually the orbit circularises. Mean motion increases, and finally the friction is so great that the orbit goes parabolic and the satellite plunges, burning up as it re�enters. Somewhat prior to that of course, it will have overheated, and the electronics will certainly fail before burn-up.
Briefly, integration of the 3 dimensional equations of motion by both direct (Cowell) and Encke's method have been used. The results here use direct integration by a Runge-Kutta-Nyström 6th order (RKN6) algorithm.
Forces modelled are Earth's gravity plus bulge terms J2, J3 and J4, the Sun and Moon, and atmospheric drag. Drag depends on the atmosphere's density, and the model documented in [1] chapter 4.4 and appendix L.3 is implemented.
The integration step size varies from approximately 100 sec at perigee to 1800 sec at apogee. At each apogee a set of osculating (kissing) keplerian elements is dumped to disc for later analysis. The program stops when the orbit goes parabolic, i.e. eccentricity < 0.
The program is written in BASIC, uses 8-byte floating-point arithmetic and runs uncompiled on an Acorn RISC Computer at a rate of 2.5 seconds computation per orbit, which is about 30 minutes per simulation year. Coding is for clarity, not speed.
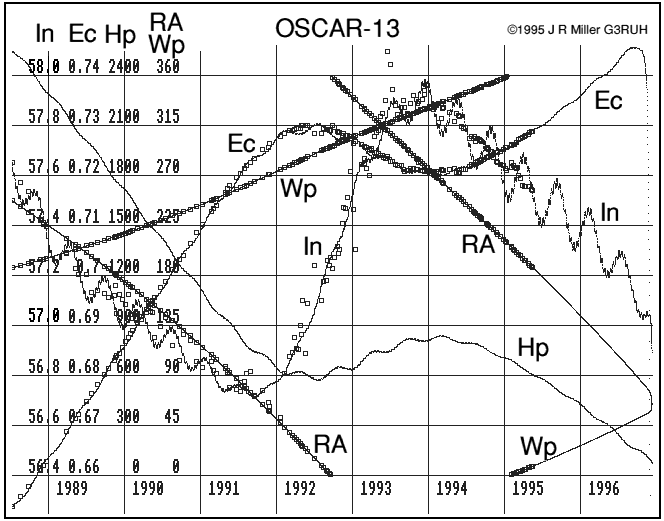
When seeded with post launch keplerian elements, the agreement with subsequent elements over the 6 years to 1994 July is within a fraction of 1°, and gives full confidence in predictions for the future. See figure 1.

Figure 1. Oscar-13 keplerian elements from launch to re-entry. Superimposed is Nasa/Norad data showing close agreement between model and reality. Abbreviations: In = Inclination deg, Ec = Eccentricity, Wp = Argument of Perigee deg, RA = Right ascension of ascending node RAAN deg, Hp = Perigee height km.
Figures for the mean density are well documented by many authors. But all caution that density is a function of several factors, including day/night, time of year, solar activity, sun's rotation, position in 11 year sun-spot cycle and so on. In consequence spot density figures on any particular day can be expected to deviate temporarily from the mean density typically 50% either way.
Clearly then it is important to examine the way Oscar-13's orbit decays with changing density. This can be be done coarsely by starting with a reference model as per [1], and then running the program with the density x0.01, x0.1, x1, x10, x100 of nominal and observing the changing outcomes.
Drag acts against the direction of motion through the atmosphere. However since the satellite is asymmetric, like an aircraft's wing it will also experience side-thrust. This is called lift. Since it is somewhat difficult to model, is hopefully small and probably averages out to zero over a perigee encounter, it has been ignored. Lift affects the orbit's orientation rather than its shape.
Half (say) of this energy is swept away by the gas, the remainder is absorbed by the satellite, which warms up.
Oscar-13 is in comfortable equilibrium with the Sun's incident energy of 500 watts. Clearly then additional heat of (say) 10x more will overheat the satellite, or at least damage the external structure, in particular the solar panels.
So as a rule of thumb, we could expect the satellite to fail through overheating when Pwr = Fd * Vr = 10 kw or so. This occurs about 3-5 weeks before re-entry.
Study of the peaks however shows them to be short lived, of duration about 100 sec, and with -10db power points spaced about +/-1.5 minutes. See figure 2 which shows this for several successive perigees that peak at 10 kw.
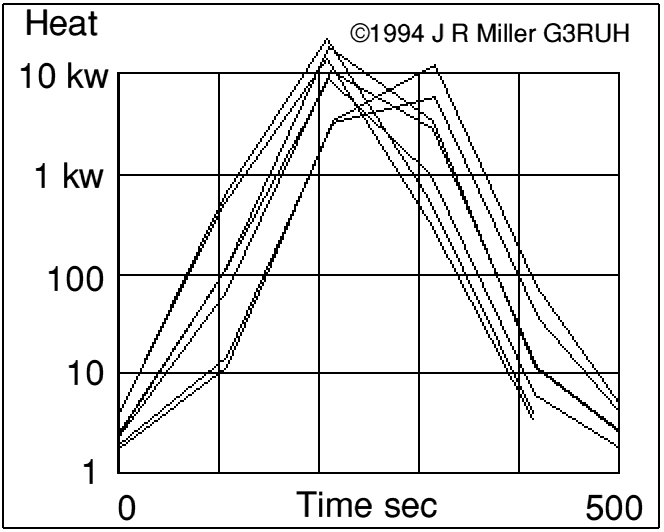
Figure 2. Profile of heating due to friction. Depicts several successive perigees peaking at the 10 kw level.
About a week before re-entry thermal heating reaches 100�kw, and exceeds 400 kw on the last orbits.
Even on the last fireball orbits, the total drag is less than 400,000/7,000 = 57 Newtons, equivalent to 6 kg weight on Earth. This force is vastly less than the satellite endured during shake testing, but when parts of it are momentarily melting one must suppose that extremities such as antennas will be swept away during this last week.
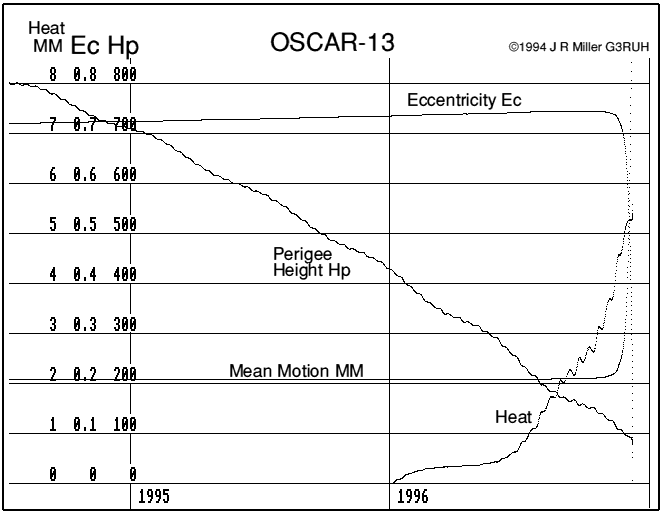
Figure 3. Nominal re-entry conditions. Abbreviations: MM = Mean motion rev/day. Heat shown as Log10 (power in watts).
From the user's point of view nothing will appear to change until about 1996 Oct 10 when peak friction reaches 500 watts which will be noticeable on the perigee telemetry. Transponder performance and satellite visibility should be exactly as they have always been. [First noted Oct 07]
Around Nov 13 peak frictional heating reaches 10 kw, and the satellite will probably fail. Changes in the eccentricity and mean motion will be just perceptible. [First solar panel failed Nov 23; satellite failed Nov 24].
Twenty-five days later, on 1996 Dec 08 the satellite re-enters. [Re-entered Dec 05]
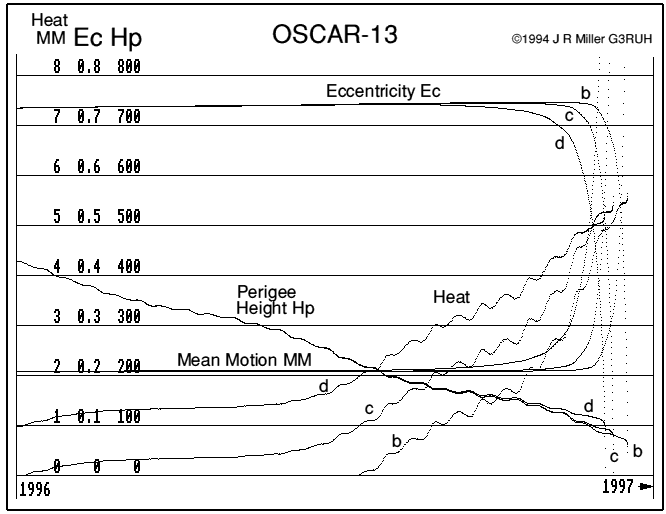
Figure 4. Last year of life with drag model scaled x0.1 (b), x1 (c), x10 (d).
In the higher drag case, decay is rather more protracted, with the 500 watt point reached on Aug 17, 15 weeks before re-entry, the 10 kw "failure" point is around Oct 28 followed by re-entry 36 days later.
If the drag is 10 times too low, the onset of heating is later, showing 500 watts on Nov 03, 6 weeks before re-entry, rapidly reaching 10 kw on Nov 24, followed by re-entry just 22 days later
The spread of re-entry dates here is 1996 Dec 03 - Dec 16.
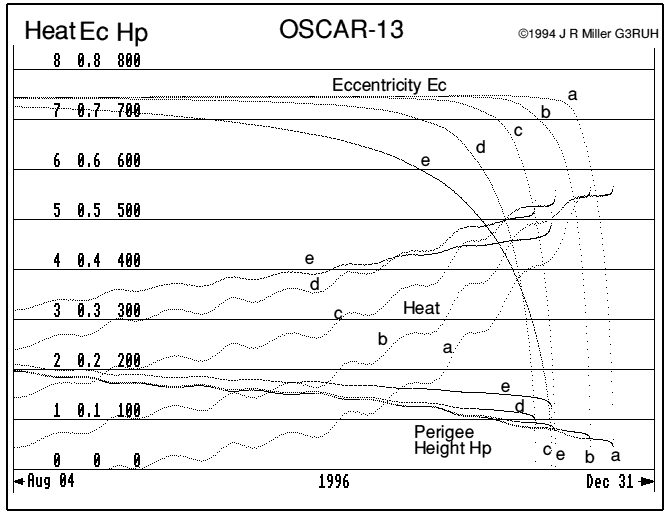
Figure 5. Last 3 months of life with drag model scaled x0.01 (a) to x100 (e).
We discover that when the drag is modelled x100 more than nominal, the re- entry date is later than for the x10 case. This is further illustrated in figure 6.
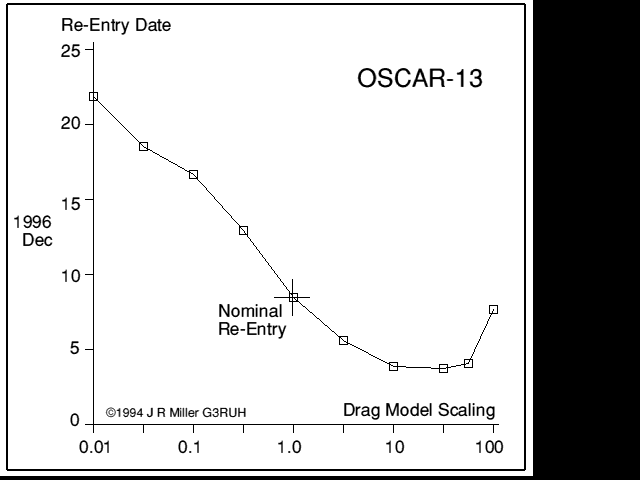
Figure 6. Re-entry date vs. drag model scaling.
From this the earliest possible re-entry date is 1996 Dec 03.
Today's hardware and software is perhaps 100x faster than that, and allows very long term analyses as well as "what-if" situations to be studied rapidly. For example, all the runs and re-runs presented in this report, plus the text, were generated in just a couple of days work.
The program listing will be seen to be very straightforward and non-mysterious. It will allow many more people to study the options for the forthcoming Phase IIID satellite. Reference [3] is already a major contribution to this field and signposts routes for further exploration.
[Added later: It was actually 1996 Dec 05 [Thu] 0854-0900 utc.]
2. Miller J.R. (G3RUH), May the Force be with You, Oscar News (UK) No. 98, 1992 Dec p 26-31. Also: The Amsat Journal (USA) 1993 Jan p16-19. Also: Satellite Operator (USA) No. 27, December 1992.
3. Kudielka V. (OE1VKW) & Drahanowsky W. (OE1WDC), Phase 3D - Feasibility Study of Launch Sequences and Orbits, OVSV, 1994 May. Austrian Radio Amateur Society, Theresiengasse 11, A-1180 Wien, Austria.
Bate, Mueller & White, Fundamentals of Astrodynamics, Dover 1971, Chapter 9.3, ISBN 0-486-60061-0.
Hoots F.R. & Roerich R.L., Models for Propagation of NORAD Element Sets, USAF Spacetrack Report Number 3, 1980 December, re-issued 1988 Dec 31 by T Kelso.
Roy A. E., Orbital Motion, Adam Hilger 1988, Chapter 7.4, ISBN 0-85274-229-0.
Weiss E. H., Tracking Earth Satellites, BYTE, 1985 July, pages 215-222.
Kudielka V. (OE1VKW), private communications 1987 July.
Kudielka V., Long term Predictions for Highly Elliptic Satellite Orbits, Amsat-DL Journal, Jun 1990. pps 5-7. (In German).
Clark T. (W3IWI) & Erricos Pavlis, The Orbital Evolution of AMSAT-OSCAR-13, Oscar News No. 84, August 1990, supplementary insert.
Clark T. & Erricos Pavlis, Chaos: The Eccentricities of Eccentric Orbits, 8th Amsat-NA Space Symposium, October 1990.
Eckart S. (DL2MDL), Orbit Stability, Proceedings 2nd P3-D Experimenters' Meeting, Marburg, Germany, May 1991. (Study of M/N orbits for P3D).
Kudielka V., Positioning a Satellite for Right Ascension and Argument of Perigee, Proceedings 2nd P3-D Experimenters Meeting, Marburg, Germany, May 1991.
Guelzow P. (DB2OS), Re-entry date of AMSAT OSCAR 13, Amsat-DL Journal, March 1992. (Presentation of the results of Clark & Pavlis, in German).
Kudielka V., Phase IIIC Orbits - Facts and Fiction, Oscar News, No. 97, October 1992, pps 41-42.
Feedback on these pages to Webmaster. Feedback on the article should be sent to James Miller
Created: 1995 May 25 -- Last modified: 2005 Oct 29